
 |
Eager Space | Videos by Alpha | Videos by Date | All Video Text | Support | Community | About |
|---|


What are gravity losses and how do they impact rocketry?
We're going to be diving into some of physics of rockets, but it's fairly simple and you don't need to understand all the details.

Let's say we are launching a Falcon 1...
We know that gravity is pushing down on the rocket at 9.81 meters per second squared.
At T=0, we fire up the engine and it starts producing thrust that pushes the rocket up. What happens?
We need to go into a bit of physics...
Remembering Newton's first law of motion, force equals mass times acceleration. In this case we know the force of the engine and the mass of the rocket, so we want to rewrite that equation as acceleration equals force / mass
Let's say that our engine produces 250 kilonewtons - or 250,000 newtons - of force and the rocket weighs 26,700 kilograms. Plug that into the formula, and we find that the engine will be producing 9.36 meters per second squared of acceleration.
9.36 is less than 9.81, so gravity is pushing down harder than the engine is pushing up. And nothing happens.
The first rule is that the upwards acceleration from the engine must be more than the downward acceleration from gravity to get off the launch pad.

Luckily, the Merlin 1A engine produces 343 kilonewtons of thrust, giving an acceleration of 12.85 meters per second squared. That is more than 9.81, so the rocket will move.
We can figure out the acceleration by subtracting the gravity from the upward acceleration, and we get 3.03 meters per second squared. That is the amount the rocket actually accelerates, the rest of the acceleration from that engine is lost to gravity. That is what a gravity loss is.

How have things changed 1 second into the flight? The rocket will be lighter because of burned propellants, but how much lighter?
That depends on the mass flow rate, which is the amount of propellant burned every second.

There are two different ways of calculating mass flow rate.
In the first method we calculate the mass flow rate from other factors. We will be talking about exhaust velocity; if you want to learn more, here's a link to a video on exhaust velocity.
It is simply the thrust in newtons divided by the exhaust velocity in meters per second. You can determine the exhaust velocity by multiplying the ISP by g, or 9.81 meters per second squared. I'll be doing the math here with detailed units so that you can see how it works.
Using the raptor as an example, it has a thrust of 1800 kilonewtons or 1800000 newtons, though that's hard to nail down as the engine is under development. It has an Isp of 333 at sea level.
Doing some math and cancelling out the units, and we determine that a raptor with 1800 kilonewtons of thrust uses 551.6 kilograms of propellant each second.
This equation is often used in reverse; if you measure the thrust of an engine and the mass flow rate, the exhaust velocity and Isp can be determined.

In the second method we use information about the rocket.
If we know how much propellant the rocket holds and how long the engines burn, we can come up with an average mass flow rate.
The Falcon 9 first stage holds 411,000 kg of propellant, and on a Starlink launch it burns for 158 seconds.
It therefore averages a mass flow rate of 2600 kilograms per second.

Now that we understand mass flow rates, we can answer our question about what happens after one second.
Based on the 343 kilonewton thrust and the Isp of 255, the mass flow rate for the Merlin 1A is 137 kilograms per second, and therefore the mass is reduced from 26,700 kilograms to 26,563 kilograms.
That increases the acceleration to 12.91 meters per second squared and the net acceleration to 3.1 meters per second squared.

This process will continue as more fuel is burned off. At 152 seconds, the last of the fuel is burned.
At that point, the mass is only 5876 kilograms, giving an acceleration of 58.37 meters per second squared.
In addition, the rocket has reached an altitude of 100 km, and that is far enough away to reduce the gravity from 9.81 meters per second squared to 9.51 meters per second squared. Do the math, and our net acceleration is 48.85 meters per second squared, or about 5 Gs of acceleration
That's how the math works. There are a few factors I ignored:
First, engines are often throttled down to a reduced thrust level to reduce the stress on the structure of the vehicle. This is very common before "Max Q", where the stress from drag is the highest.
Second, engines get more efficient as the move out of the atmosphere. For the Merlin 1A, the thrust will increase from 343 kilonewtons to 409 kilonewtons in vacuum and the actual acceleration will be around 6 Gs
Third, engines are sometimes throttled down at the end of their burn to keep the acceleration from being too high for the payload or vehicle.
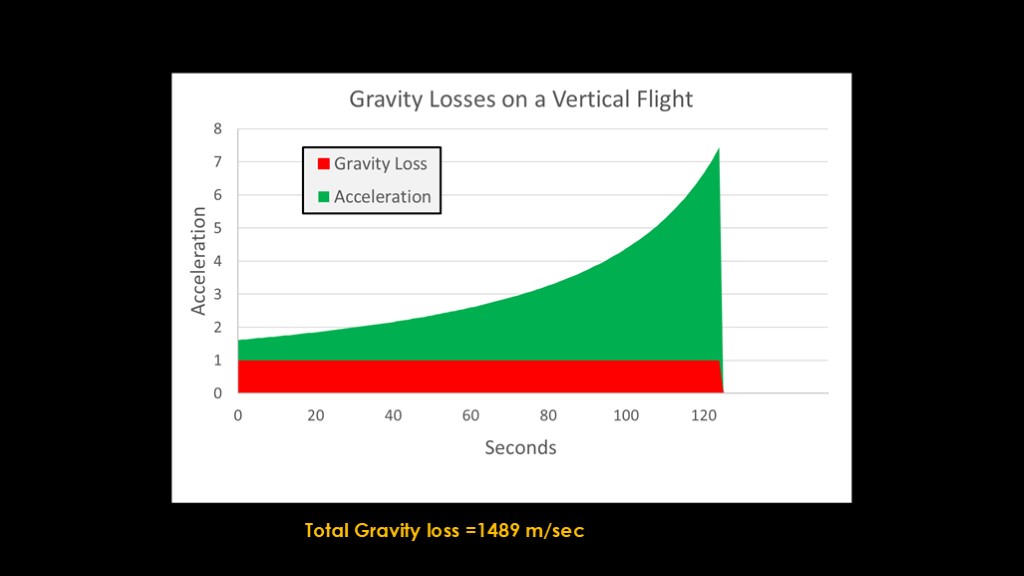
Here's a chart that shows what is going on, with the red section showing the gravity losses. You need to pay the gravity tax before you can get any useful work accomplished.
If we add up the total gravity loss for this booster flight, it turns out to be 1489 meters per second.
Is there a way to reduce gravity losses?

We can switch to the Merlin 1C engine, which produces 423 kN, or 23% more thrust than the Merlin 1A. That nearly doubles the net acceleration.
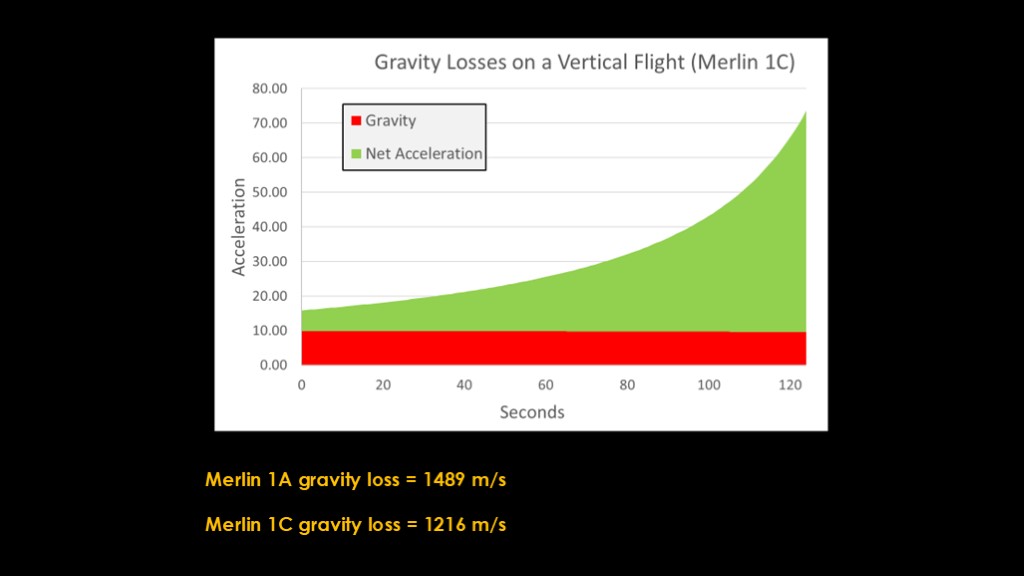
Here we can see the effect. The Merlin 1C burns the propellant faster so it's done in only 125 seconds and only wastes 1216 meters per second on gravity losses. That is great.
Then some bozo comes along and says, "you know, we can upscale the rocket to hold 23% more propellant and take advantage of the higher thrust to launch bigger payloads", and that extends the burn time back to where it was and you end up losing about the same amount to gravity losses.
The summary here is that gravity losses are just something you have to deal with.

Orbital flight adds more complexity.
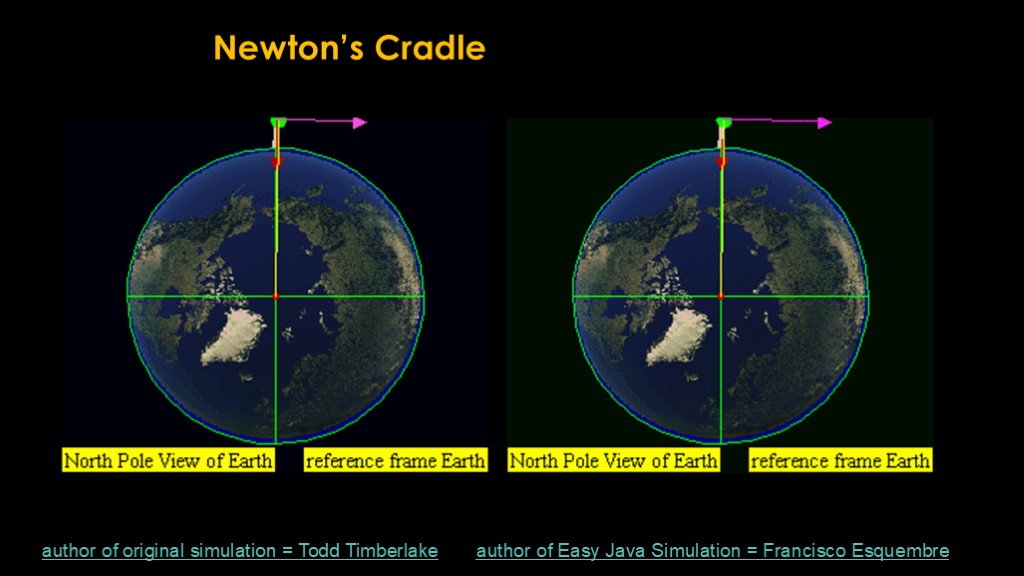
This is a classical thought experiment known as Newton's Cradle. It involves shooting a cannonball horizontally from a cannon on a very high mountaintop.
What we see is that if the cannonball has a lot of horizontal velocity, it will take some time before it will impact the earth because the earth curves away from it.
In this right image, we see if that horizontal velocity is high enough, the rate at which gravity pulls the cannonball closer to the earth is exactly balanced by the rate at which the earth curves away. That is what it means to be in orbit.

How does this relate to gravity losses?
This is a velocity chart of a Falcon 9 on the Crew 1 mission to the international space station.
The black line shows the total velocity; you can see that it starts slow but increases as the first stage burns off fuel, then flattens out as the second stage takes over.
We can add two more lines to show the vertical and horizontal components.
The blue line shows the vertical velocity; note that the first stage builds up a lot of vertical velocity, and then that vertical velocity bleeds away from gravity losses as the launch continues. This makes sense as the goal when launching to a specific altitude is to reach that altitude with zero vertical velocity. The first stage also builds up some horizontal velocity, but not that much.
The second stage then primarily handles adding enough horizontal velocity to get into orbit.

Knowing what we know about Newton's cradle - that the faster we go the more the earth curves away - how does that effect gravity losses?
This chart shows the horizontal velocity in green and the gravitational constant in yellow. The gravity starts at 9.8 and goes down to 9.2 as the launcher gets farther away from the earth - that is the same effect shown in the previous charts. It's a small effect, only about a 6% reduction.

Now we can add in the effect based on velocity.
The red line shows the effective gravity loss - the amount of acceleration we need to stay at the same altitude. As we go faster - as we near orbital speed - it reduces significantly.
For a flight into orbit, we would expect that the red line would go all the way down to zero. But for crewed flights, the capsules are typically launched so their speed is just a little bit less than orbital speed - about 250 m/s less - so that if there are problems with the capsule's thrusters, the capsule will reenter naturally.

That's the story on gravity losses
(read)

A huge thank you to Declan Murphy for FlightClub.io, a wonderful reference if you want to dig in deeper into these sorts of issues.

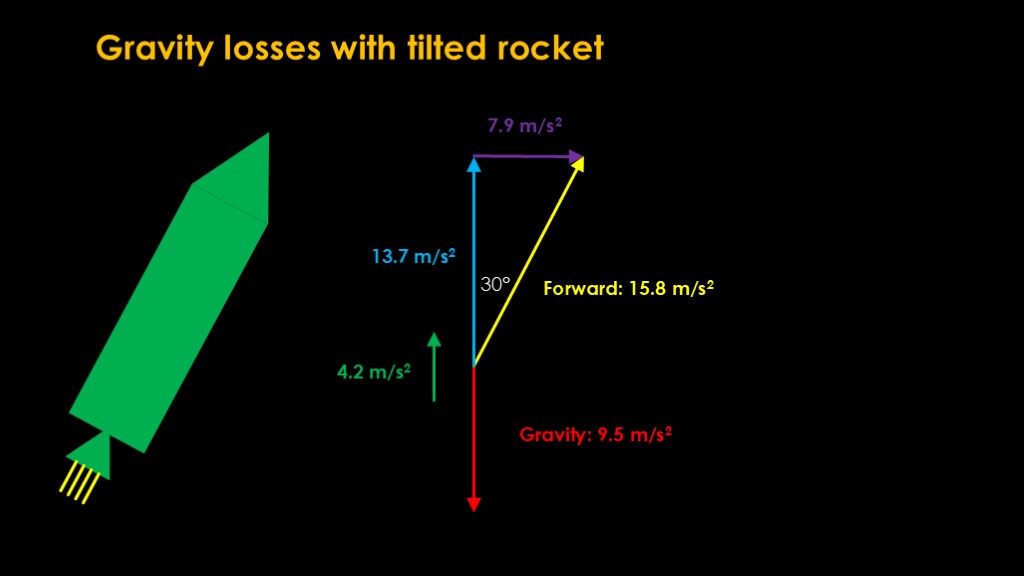
When the rocket is tilted, part of the acceleration is up and part of it is to the side.
In this diagram, gravity is pulling down at 9.5 meters per second squared, and the rocket is thrusting forward at 15.8 meters per second squared.
Doing a bit of math, we discover that the rocket is accelerating up at 13.7 meters per second squared and to the side at 7.9 meters per second squared. The upwards acceleration is countered by gravity, producing a net upwards acceleration of only 4.2 meters per second squared.